一元函数微分学的概念
1 选择中常出现的一些知识点
Error
函数在一点处可导/连续,无法得到{1: 其在该点周围可导/连续}。这在一些选择题中举反例很重要。
导数存在,该点处切线一定存在,但反之则{1: 不成立}。
对于一元函数而言,可导{1: 必可微},
- 若
在点 处有二阶导数,则 在 的某个邻域内有{1:一阶导数,且一阶导数在 处连续}。 - 若
在点 处有 阶导数,则 在 的某个邻域内有{1: 阶的各阶导数}。
- 设
在 处连续,则 在 处连续,反之,则不成立。 - 若
在 处可导,若 ,则带绝对值后仍可导,若 ,则只有{1: }时可导。 - 注:结合绝对值函数来记忆。
导函数是性质很强的函数,当导函数极限存在时,导函数在这一点处{1: 连续}。但函数没有此性质。即可以推论得到,如果一点处导函数存在,那这一点一定不是{1: 第一类间断点}。同理,如果函数可导,那么导函数可能{1: 连续或有振荡间断点}。
2 可微
可微的判别
- 写增量
- 写线性增量:
- 做极限:
- 若{1: 极限为 0},则
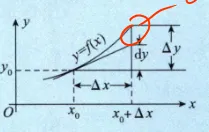
在点 处可微,否则不可谓 - 可微的几何意义如下,选择题来画图有奇效。