函数极限与连续

1 函数的性质

1.1 反函数

反函数存在的前提为单值函数，严格单调函数必有反函数。原函数和反函数的图像{1: 完全重合，只有把 xy 互换，图形才关于 y=x 对称}。

1.2 函数的奇偶性

函数的奇偶性主要用于计算过程中的简化，对于复合函数来说，{1: 内偶则偶，内奇函同外}。若一个函数 $f (x)$ 为偶函数，则对他求导，奇偶性发生改变。其积分 {1: $\int_{0}^{x} f (t) d t$ } 奇偶性发生改变。

对于任意的 x,y，都有 $f (x + y) = f (x) + f (y)$ ，则 $f (x)$ 为{1: 奇函数}。

1.3 函数的周期性

若 $f (x)$ 是以 T 为周期的可导函数，则求导周期不发生改变。但只有{1: 在一个周期内积分为 0，即 $\int_{0}^{T} f (x) d x = 0$ }，此时 $\int_{0}^{x} f (x) d x = 0$ 的周期不变，反之，则不成立。

对于正弦函数和余弦函数，一拱的面积{1: 为 2}.

1.4 凹凸性

对于凹凸性，主要掌握余项放缩和凹凸性不等式，例如，如果 $f^{''} (x) > 0$ ，则余项放缩为{1:： $f (x) = f (0) + f^{'} (0) x + f^{''} (0) x^{2} \geq f (0) + f^{'} (0) x$ }，凹凸性不等式：{1: $f (x) ⩽ f (a) + \frac{f (b) - f (a)}{b - a} (x - a)$ }

1.5 函数中不熟悉的公式

三角函数公式

正割函数（偶函数）： $\sec x = \frac{1}{\cos x}$
- {1: $1 + \tan^{2} α$ } $= \sec^{2} α$
余割函数（奇函数）： $\csc x = \frac{1}{\sin x}$
- {1: $1 + \cot^{2} α$ } $= \csc^{2} α$

对于反三角函数来说，例如 $\sin (\arccos x)$ ，要利用画图来合理计算，每必要记公式了。

反三角函数公式

{1: $\arcsin x + \arccos x$ } $= \frac{π}{2} (- 1 ⩽ x ⩽ 1) .$
{1: $\arctan x + a r c c o t x$ } $= \frac{π}{2} (- \infty < x < + \infty) .$

2 函数极限的性质

唯一性：如果极限存在，那么极限唯一。
- 函数极限存在的充要条件为{1: 左右极限存在且相等}。
- $lim_{x \to x_{0}} f (x) = A \Leftrightarrow f (x) = A + α (x)$
局部有界性：
- 有界函数的和差积均为有界函数。
局部保号性：
- 脱帽{1: 严格不等}，戴帽{1: 非严格不等}，即 $lim f > 0 \Rightarrow f > 0$ ， $f ⩾ 0 \Rightarrow lim f ⩾ 0$

3 计算方法

计算时碰到分子或者分母出现两个函数相减的情况，一般思路考虑优先提取公因式，凑常见等价无穷小，或者进行洛必达。碰到三角函数、反三角函数、对数函数之差时，可以考虑拉格朗日中值定理处理之后在计算。若较为复杂的式子在分子上，可以考虑泰勒公式进行计算，在分母上一般不考虑。

3.1 洛必达法则

洛必达法则是用来计算未定式的，使用洛必达法则的前提{1: 是分子分母在趋向值 a 的某去心邻域内导数存在且分母的导数值不为 0}，对洛必达法则而言，等式右侧存在，则左存在，反之则不成立。洛必达有时候也有可能反推进行计算，例如 $lim_{x \to 0} \frac{\cos x - \cos (\sin x)}{x (e^{x^{3}} - 1)} = lim_{x \to 0} \frac{\int_{x}^{\sin x} \sin t d t}{x^{4}} = lim_{x \to 0} \frac{\int_{x}^{\sin x} t d t}{x^{4}}$ ，然后通过中值定理去求解会更简单一些。

3.2 泰勒公式

使用泰勒公式的前提是{1: $f (x)$ 在 $0$ 点处 $n$ 阶可导}。且只在 x=0 的一个邻域内满足：{1: $f (x) = f (0) + f^{'} (0) x + \frac{f^{″} (0)}{2!} x^{2} + \dots + \frac{f^{(n)} (0)}{n!} x^{n} + o (x^{n}) .$ }

常用泰勒公式含佩亚诺余项

$\sin x =$ {1: $x - \frac{x^{3}}{3!} + o (x^{3}),$ }
$\cos x =$ {1: $1 - \frac{x^{2}}{2!} + \frac{x^{4}}{4!} + o (x^{4})$ }
$\arcsin x =$ {1: $x + \frac{x^{3}}{3!} + o (x^{3}),$ }
$\tan x =$ {1: $x + \frac{x^{3}}{3} + o (x^{3}),$ }
$\arctan x =$ {1: $x - \frac{x^{3}}{3} + o (x^{3}),$ }
$\ln (1 + x) =$ {1: $x - \frac{x^{2}}{2} + \frac{x^{3}}{3} + o (x^{3}),$ }
$e^{x} =$ {1: $1 + x + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + o (x^{3}),$ }
$(1 + x)^{α} =$ {1: $1 + α x + \frac{α (α - 1)}{2!} x^{2} + o (x^{2})$ }
注意其奇偶性，只有 $s i n x, c o s x, e^{x}$ 的展开式中有阶乘。泰勒多项式不含有高阶无穷小。
在计算过程中出现泰勒多项式的相除的情况下，尽可能将其转换为乘法，或转换成常见函数的形式再次使用泰勒公式进行计算。直接使用长除法很难把握。

泰勒公式含有高阶无穷小计算时，加减法时{1: 低阶吸收高阶}，乘法时{1: 阶数累加}。

泰勒公式的常见错误

如果给出的函数含有无穷小，则{1: 不能直接使用求导公式}，其在 $x \neq 0$ 时， $f (x)$ 处处不连续。只能用定义来进行求解。（ $f (x) = 1 + x^{2} + x^{2} ∙ x D (x) = 1 + x^{2} + o (x^{2})$ ）

3.3 等价无穷小

常见等价无穷小（x

\to

0） #anki

$\ln (x + \sqrt{x^{2} + 1}) \sim x$
$\sin x \sim \tan x \sim \arctan x \sim \ln (1 + x) \sim e^{x} - 1 \sim x$
$(1 + x)^{α} - 1 \sim α x (α \neq 0)$
$a^{x} - 1 \sim x \ln a$
$1 - \cos^{a} x \sim \frac{1}{2} a x^{2}$
$x - \sin x \sim \frac{1}{6} x^{3}$
$\arcsin x - x \sim \frac{1}{6} x^{3}$
$\tan x - x \sim \frac{1}{3} x^{3}$
$x - \arctan x \sim \frac{1}{3} x^{3}$
$x - \ln (1 + x) \sim \frac{1}{2} x^{2} \sim 1 - \cos x$
$(1 + x)^{\frac{1}{x}} - e \sim \frac{e}{2} x$
$e^{x} - 1 - x \sim \frac{1}{2} x^{2}$

只有能够整体提出的部分才能进行等价无穷小的代换，即如果出现加减或出现带入后为 0 的情况下，则不能直接进行等价无穷小的代换。如果 $lim f (x) = 0$ ，则不能进行直接拆开计算，只能看是{1: 否为无穷小 $\times$ 有界}。

函数的等价无穷小 #anki

当 $x \to 0$ 时, $f (x) \sim a x^{m}, g (x) \sim b x^{n}, a b \neq 0, m, n$ 为正整数,则 $f [g (x)] \sim a b^{m} x^{m}$
当 $x \to 0$ 时, $f (x) \sim a x^{m}, a \neq 0, m$ 为正整数,则 $\int_{0}^{x} f (t) d t \sim \int_{0}^{x} a t^{m} d t .$
若 $lim_{x \to 0} f (x) = A \neq 0, lim_{x \to 0} h (x) = 0$ 且在 $x \to 0 时, h (x) \neq 0, 则当 x \to 0 时 \int_{0}^{h (x)} f (t) d t \sim A h (x) .$
当 $x \to 0$ 时, $f (x) \sim a x^{m}, g (x) \sim b x^{n}, a b \neq 0, m, n$ 为正整数,则 $\int_{0}^{g (x)} f (t) d t \sim \int_{0}^{b x^{n}} a t^{m} d t$
上述 $m, n$ 均为正整数，如果是正实数，则在 $x \to 0 +$ 时，该结论依旧成立。

3.4 夹逼准则

夹逼准则主要记一些不等式，然后不要过度放缩，感觉这个度是比较难以掌握的。

3.5 单调有界准则

单调有界准则用来证明极限存在，然后设该极限为 A，带回后计算。其核心还是在放缩方面。选填注意一下这个函数：

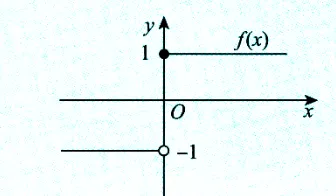
4 函数的连续与间断

讨论函数的间断点只需要关注无定义点和分段点。左右极限{1: 存在且相等时}，函数在该点连续。对于复合函数而言，{1: 内外都在该点处连续}才能说函数在该点处连续。且反函数与原函数有{1: 相同的单调性和连续情况}。

5 重要的等式与不等式

等式 #anki

$a^{2} + b^{2} + c^{2} = (a + b + c)^{2} - 2 (a b + b c + a c)$
$a^{2} + b^{2} + c^{2} + a b + b c + a c = \frac{1}{2} [(a + b)^{2} + (b + c)^{2} + (a + c)^{2}]$
$1 + \sin 2 θ = (\sin θ + \cos θ)^{2}$
$\tan (α + β) = \frac{\tan α + \tan β}{1 - \tan α \tan β}$
高次因式分解
- $a^{2} + a b + b^{2} = \frac{a^{3} - b^{3}}{a - b}$
- $a^{2} - a b + b^{2} = \frac{a^{3} + b^{3}}{a + b}$
- 当 $n$ 为正整数时， $a^{n - 1} + a^{n - 2} b + \dots + a b^{n - 2} + b^{n - 1} = \frac{a^{n} - b^{n}}{a - b}$
- 当 $n$ 为正奇数时， $a^{n - 1} - a^{n - 2} b + \dots - a b^{n - 2} + b^{n - 1} = \frac{a^{n} + b^{n}}{a + b}$
$1^{k} + 2^{k} + \dots + n^{k} = \frac{1}{k + 1} n^{k + 1} + R_{k}$ （常用于放缩）

不等式 #anki

$0 ⩽ a + ∣ a ∣⩽ 2 ∣ a ∣$
$∣ a - b ∣=∣ a - c + c - b ∣⩽∣ a - c ∣ + ∣ c - b ∣$
$\frac{2}{\frac{1}{a} + \frac{1}{b}} ⩽ \sqrt{a b} ⩽ \frac{a + b}{2} ⩽ \sqrt{\frac{a^{2} + b^{2}}{2}}$ ，其中 $a, b > 0$ .
$| a b | ⩽ \frac{a^{2} + b^{2}}{2} .$
$(a + b) (\frac{1}{a} + \frac{1}{b}) ⩾ 4$ ，其中 $a, b > 0$ .
$\frac{a^{2}}{c} + \frac{b^{2}}{d} ⩾ \frac{(a + b)^{2}}{c + d} (a, b, c, d > 0)$ ，以 $k_{1} a^{2} + k_{2} b^{2}$ 为目标进行放缩。
$\frac{a + b + c}{3} ⩾ \sqrt[3]{a b c} (a, b, c > 0)$
$\frac{(b - a)^{2}}{2} ⩽ (x - a)^{2} + (b - x)^{2} ⩽ (b - a)^{2}, x \in [a, b]$
$\frac{(b - a)^{3}}{4} ⩽ (x - a)^{3} + (b - x)^{3} ⩽ (b - a)^{3}, x \in [a, b]$
$(a_{1} b_{1} + a_{2} b_{2})^{2} ⩽ (a_{1}^{2} + a_{2}^{2}) (b_{1}^{2} + b_{2}^{2}) (柯西不等式)$ 可以推导出 ${[\int_{a}^{b} f (x) g (x) d x]}^{2} ⩽ \int_{a}^{b} f^{2} (x) d x • \int_{a}^{b} g^{2} (x) d x$
$0 < a < 1 \Rightarrow (1 - a)^{n} - (1 - a)^{n + 1} = (1 - a)^{n} (1 - 1 + a) = (1 - a)^{n} ∙ a > 0 .$ （学会去反向凑）

初等函数不等关系 #anki

$e^{x} ⩾ x + 1 \Rightarrow e^{\circ} ⩾ ◻ + 1, 如: e^{x - 1} ⩾ x$
$e^{x} ⩾ e x$
$1 - \frac{1}{x} ⩽ \ln x ⩽ x - 1$
$当 0 < x < 1 时, \frac{x}{x + 1} ⩽ \ln (1 + \frac{1}{x}) ⩽ \frac{1}{x} .$
$e^{x} - \ln x > 2$
$\sin x < x < \tan x, x \in (0, \frac{π}{2}) .$
$\arctan x ⩽ x ⩽ \arcsin x (0 ⩽ x ⩽ 1)$
$∣ \cos x ∣= | \sin (\frac{π}{2} - x) | ⩽ | x - \frac{π}{2} |$
$\frac{2}{π} < \frac{\sin x}{x} < 1, x \in (0, \frac{π}{2})$
$1 < \frac{\tan x}{x} < \frac{4}{π}, x \in (0, \frac{π}{4})$
${(1 + \frac{1}{x})}^{x} < e, x > 0$
$x \ln x ⩾ - \frac{1}{e}, x > 0$
$当 n \to \infty 时, 有 \ln^{α} n ≪ n^{β} ≪ a^{n} ≪ n! ≪ n^{n}, 其中 α, β > 0, a > 1$